Linea de Bézier
LINEAS DE BÉZIER
Se denomina curvas de Bézier a un sistema que se desarrolló hacia los años 1960 para el trazado de dibujos técnicos, en el diseño aeronáutico y en el de automóviles. Su denominación es en honor a Pierre Bézier, quien ideó un método de descripción matemática de las curvas que se comenzó a utilizar con éxito en los programas de CAD.
Se denomina curvas de Bézier a un sistema que se desarrolló hacia los años 1960 para el trazado de dibujos técnicos, en el diseño aeronáutico y en el de automóviles. Su denominación es en honor a Pierre Bézier, quien ideó un método de descripción matemática de las curvas que se comenzó a utilizar con éxito en los programas de CAD.
La generalización pasaría a ser las curvas denominadas "Spline", es decir la curva de Bézier es un Spline de tercer grado. La curva de Bézier de grado  puede ser generalizada de la siguiente manera. Dados los puntos P0, P1,..., Pn, la curva de Bézier es del tipo:
puede ser generalizada de la siguiente manera. Dados los puntos P0, P1,..., Pn, la curva de Bézier es del tipo:
Por ejemplo, una curva de orden cinco ( ) quedaría como:
) quedaría como:
Esta ecuación puede ser expresada de manera recursiva como sigue: sea la expresión  que denota la curva de Bézier determinada por los puntos P0, P1,..., Pn. Entonces
que denota la curva de Bézier determinada por los puntos P0, P1,..., Pn. Entonces
En otras palabras, el grado  de la curva de Bézier es una interpolación entre los dos grados
de la curva de Bézier es una interpolación entre los dos grados  de las curvas de Bézier.
de las curvas de Bézier.
Terminología
Existe una terminología asociada exclusivamente para este tipo de curvas. Se tiene:
donde las polinomiales
son conocidas como polinomios de Bernstein de grado n, definidos por 00 = 1.
Los puntos Pi son llamados puntos de control de las curvas de Bézier. El polígono formado por la conexión de los puntos de Bézier con rectas, comenzando por P0 y terminando en Pn, se denomina polígono de Bézier (o polígono de control). La envolvente convexa del polígono de Bézier contiene las curvas de Bézier.
Notas
- La curva de Bézier se encuentra en el interior de la envolvente convexa de los puntos de control.
- La curva de Bézier es infinitamente derivable.
- El control de la curva es global. Modificar un punto de control implica modificar completamente la curva.
- Para efectuar una transformación afín de la curva es suficiente efectuar la transformación sobre todos los puntos de control.
- La curva comienza en el punto P0 y termina en el Pn. Esta peculiaridad es llamada interpolación del punto final.
- La curva es un segmento recto si, y solo si, todos los puntos de control están alineados.
- El comienzo (final) de la curva es tangente a la primera (última) sección del polígono de Bézier.
- Una curva puede ser desdoblada en algunos puntos en dos curvas, o de manera arbitraria en tantas curvas como se quieran, cada una de las cuales es una nueva curva de Bézier.
- Algunas curvas que parecen simples, tales como una circunferencia, no pueden ser descritas de manera exacta mediante curvas de Bézier o segmentos de esta clase de curvas (por raro que parezca una curva formada a su vez por cuatro segmentos de curva puede aproximarse a un círculo, con un error radial máximo menor de una parte por mil, en cada punto de control interno la distancia es
de manera horizontal o vertical de un punto de control del exterior sobre el círculo unidad).
- La curva compensada obtenida a partir de una curva de Bézier dada, frecuentemente llamada curva compensada (falsa "paralela" a la curva original, como los raíles en una vía de tren) no puede ser trazada de manera exacta mediante curvas de Bézier. De todas formas hay métodos heurísticos que proporcionan, normalmente, una aproximación adecuada en algunos propósitos prácticos.


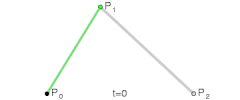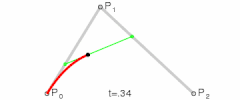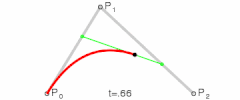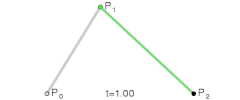

![Animación t en el intervalo [0,1]](https://upload.wikimedia.org/wikipedia/commons/thumb/d/db/B%C3%A9zier_3_big.gif/240px-B%C3%A9zier_3_big.gif)

![Animación, t en el intervalo [0,1].](https://upload.wikimedia.org/wikipedia/commons/thumb/a/a4/B%C3%A9zier_4_big.gif/240px-B%C3%A9zier_4_big.gif)





Comentarios
Publicar un comentario